Concepto
Es un método que es utilizado cuando existe un
problema donde se debe realizar varios viajes a diferentes lugares una sola vez y se debe llegar al mismo lugar de donde se
originó dicho viaje. Es por ello que los principales objetivos son minimizar
distancias, tiempos y costos, es decir, que al realizar una secuencia entre
varios nodos estos pueden ser estaciones, ciudades, puntos de referencia entre
otros.
Para realizar un problema de agente viajero, es necesario tomar en cuenta donde están dadas las n ciudades y el costos Cij que se genera al viajar de una ciudad a otra.
Siguiendo con la definición del Agente Viajero (PAV) o bien traveling salesman problem (TSP) Nombre de referencia a nivel mundial.
Para realizar un problema de agente viajero, es necesario tomar en cuenta donde están dadas las n ciudades y el costos Cij que se genera al viajar de una ciudad a otra.
Tomando como finalidad
al realizar el ejercicio lo siguiente:
- Conseguir el recorrido más corto en n ciudades.
- Cada ciudad solo puede ser visitada una sola vez antes de llegar de nuevo al punto de partida.
- Minimizar tiempo, y costos.
Siguiendo con la definición del Agente Viajero (PAV) o bien traveling salesman problem (TSP) Nombre de referencia a nivel mundial.
Este tipo de
problema es estudiado en la Investigación de Operaciones y en la optimización combinatoria tomado como
uno de los problemas principales de gran importancia. Estos de problemas son
utilizados como base para resolver una gran
cantidad de problemas que ocurren en la vida cotidiana. Por otro lado también
es utilizado en otra área tal como la teoría de la complejidad
computacional para aprobar algoritmos que se van descubriendo día
a día.
Sumado a esto otra de las áreas
en las que se puede observar el problema del agente viajero es en la teoría de
gráficas. En la siguiente grafica se puede observar las tres grandes áreas o
enfoques que ha tomado el problema del Agente Viajero para su estudio, véase
el siguiente gráfico. http://www.scribd.com/doc/104889745/Agente-Viajero-
Si
como objetivo se quiere minimizar el tiempo usado para la configuración de una máquina que es usada para producir n cantidad de artículos, se le llama TSP,
y cada nodo corresponde a cada uno de los diferentes artículos y la distancia al ir a modificar la maquina es el tiempo
usado en la modificación de una maquina a la otra.
Cuando
el objetivo no es reducir el tiempo o el recorrido en distancia al realizar el
viaje, es necesario medir el costo que se obtiene al realizar dicho recorrido. Este
en algunos casos suele ser más importante que los otros dos factores ya mencionados.
Ahora
bien para tener una referencia que muestre de manera práctica y conceptual la
definición del Agente Viajero, se ha utilizado el libro de Investigación de Operaciones Hamdy Taha. Séptima edición. Año 2004.
En la sección 5.4 y 9.2 para los algoritmos. Donde se hace referencia de que
dicho problema tiene que ver con la determinación del viaje más corto en un
caso, con n ciudades a visitar, en el
cual cada ciudad se visita exactamente solo una vez. Es por ello que el
problema del Agente Viajero es un modelo de asignación con limitaciones
adicionales que aseguran la exclusión de sub-viajes en la solución óptima.
Entonces se debe tomar en cuenta de forma específica en el caso del problema
del Agente Viajero con n ciudades, lo
siguiente:

Si dij
es la distancia de la ciudad i a la
ciudad j, el modelo del agente
viajero es el siguiente:
· Las restricciones
(1),(2),(3) definen un modelo regular de asignación.
En general, el problema
de asignación producirá soluciones de subcircuito, más que un circuito completo
que abarque todas la n ciudades.
A continuación se
presenta un modelo con 5 ciudades. Los arcos representan las rutas en dos
sentidos. Por otro lado se puede observar que la solución del circuito y dl
subcircuito del modelo de asignación asociado. Si las asignaciones forman una solución del circuito, el circuito es óptimo. En caso contrario
se agregan más restricciones al modelo de asignación para eliminar los sub-circuitos.
Las siguientes imágenes son tomadas del libro de Investigación de Operaciones
de Hamdy Taha. Séptima
edición. Año 2004. En la sección 5.4 y 9.2 para los algoritmos.
Ahora bien los métodos
disponibles para resolver el problema del agente viajero tienen su base en las
ideas de los algoritmos generales de ramificación y acotamiento o del plano de
corte.
Para tener una idea más
clara acerca del método de asignación es importante leer del libro Investigación de Operaciones de Hamdy
Taha. Séptima edición. Año 2004. En la sección 5.4 y 9.2 para los algoritmos.
Definiciones
y ejemplos tomados del libro Investigación de Operaciones. Hamdy A Taha Séptima
edición. Año 2004. Pág. 390, 391.
Como parte del
aprendizaje del tema Agente Viajero, en el siguiente video se explica de manera
sencilla como realizar dicho problema.
Áreas en las que al aplicar el problema del agente viajero y
resulta muy útil
El problema del Agente Viajero se puede emplear en
cualquier situación que requiera seleccionar nodos en cierto orden que reduzca
los costos en las áreas de:
- · Reparto de productos: Con la finalidad de mejorar una ruta de entrega para así conseguir la más corta.
- · Transporte: Ya que permite realizar la mejor selección del recorrido de caminos buscando la menor distancia.
- · Robótica: Utilizado con el objetivo de resolver problemas de fabricación de equipos o productos para así minimizar el número de desplazamientos al realizar una serie de perforaciones en un circuito impreso.
- · Horarios de transportes laborales y/o escolares: Permitiendo de este modo estandarizar los horarios en los transportes, ya que es una de sus aplicaciones principales, tanto así que actualmente existen empresas que se especializan en ayudar a las escuelas a programar el tiempo y recorrido para optimizarlos en base a una solución del TSP.
- · Inspecciones a sitios remotos: En esta área es utilizado ya que permite ordenar los lugares que deberá visitar un inspector en el menor tiempo posible.
·
Secuencias: Aquí su uso consiste hacer
referencia al orden en el cual n
trabajos tienen que ser procesados de tal forma que se minimice el costo total
de producción.
http://www.posgradoeinvestigacion.uadec.mx/CienciaCierta/CC30/3.html
Visto de esta manera el
problema del Agente Viajero es de gran utilidad. Es aplicado para reducir los
costos al realizar un recorrido por varias áreas una sola vez partiendo desde
un punto y terminado en el mismo lugar, de manera que se quiere logra reducir
los costos al realizar dicha actividad y recortar en términos de tiempo o
distancia el viaje.
En el Problema del Agente Viajero, la solución al
problema es una permutación de las n
ciudades dadas, y este es dividido en dos tipos:
Ø TSP simétrico (STSP): Al realizar este método la matriz de costos Cij es
simétrica, es decir, que, el costo que se genera viajar de la ciudad i a la
ciudad j es el igual al que se tiene al viajar de la ciudad j a la
ciudad i.
Ø TSP asimétrico (ATSP): En este caso, la matriz de costos Cij no
es simétrica, es decir, que, el costo que se genera de viajar de la ciudad i a
la ciudad j, en general, no es el i que igual que se obtiene al
viajar de la ciudad j a la ciudad i.
Para ambos casos la formulación matemática es la
igual, con la diferencia de que la matriz de costos para el primero es
simétrica, y para el segundo no es igual. De manera que se han desarrollado
formulaciones matemáticas específicas para el segundo caso. En las
aplicaciones, tanto el caso simétrico como el asimétrico son de gran
importancia.
El Problema del Agente Viajero en su forma
asimétrica tiene (n-1)! rutas disponibles, esto es, (n-1)! posible soluciones.
La forma simétrica tiene recorridos, porque al modificar la dirección de la
ruta ésta no cambia y sigue siendo la misma.
Ahora bien, la parte simétrica ha sido más explorada en la investigación y desarrollo de algoritmos para resolver el TSP.
Al resolver un problema
del agente viajero sebe tomar en cuenta todos los métodos que pueden aplicarse.
El
Problema del Agente Viajero puede resolverse de diferentes maneras:
Ø Enumeración de todas las soluciones factibles: Es decir, se debe enlistar todas
las posibles soluciones del problema, calcular los costos asociados,
identificar por comparación, cuál es la solución con el costo más acorde, más
bajo.
Ø Métodos exactos: Son llamados algoritmos óptimos, con estos se intenta descartar
familias de las posibles soluciones, tratando siempre de acelerar la búsqueda y
llegar a una solución óptima. Los métodos que más se usan para resolver el TSP
son Ramificación y Acotamiento, Ramificación y Corte.
Ø Heurísticas: Estos son
métodos que obtienen buenas soluciones
en tiempos de cómputo muy cortos, sin embargo no se puede garantizar el punto
óptimo de la solución.
Existen diferentes tipos de heurísticas (Glover,
Gutin, Yeo y Zverovich, 2001):
Ø Heurísticas constructivas: Son procedimientos que se encargan de obtener una
solución a partir de un criterio inicial, consiste en construir una solución
factible.
Ø Heurísticas de búsqueda local: Aquí son aplicados los procedimientos para mejorar
soluciones ya encontradas. Es decir, que tratan de optimizar localmente
alrededor de una solución, ubicando mínimos locales.
Ø Heurísticas combinadas: Utilizado como procedimiento que constan de una
heurística constructiva y una heurística de búsqueda local.
Heurística para el Problema del Agente Viajero
(Cirasella, Lyle, McGeoch y Zhang, 2000):
El vecino más cercano (heurística constructiva)
Este tipo de heurística consiste en la idea de moverse de una ciudad a la siguiente, de tal manera que, de todas las opciones, la ciudad elegida sea la más cercana a donde se haya ubicado el agente viajero. Es considerada como una heurística miope, ya que en una iteración 3 escoge entre ellas la mejor opción que tiene disponible, sin ver que esto puede forzar a tomar malas decisiones posteriormente (Johnson et al., 2002).
Ilustración
2. El vecino más
cercano, heurística constructiva.
http://www.posgradoeinvestigacion.uadec.mx/CienciaCierta/CC30/3.html
El Problema del Agente Viajero o TSP es un problema
calificado como difícil de resolver, propiamente dicho como NP-Completo. Es decir,
es un problema para el cual no podemos garantizar que se encontrará la mejor
solución en un tiempo de cómputo razonable, por esto, cuando una instancia de
grandes dimensiones se resuelve con algún método exacto, toma un extenso
periodo de tiempo de estudio. Con el uso de heurísticas se tienen soluciones de
muy buena calidad en tiempos de cómputo mucho más pequeños.
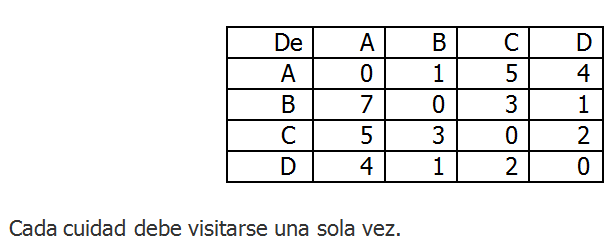
Un viajero tiene que visitar cada una de las cuatro
ciudades y lo quiere hacer de tal manera que visite una sola vez partiendo de
la ciudad A y regresando al final del recorrido, viajando el menor tiempo
posible, la siguiente tabla muestra los tiempos entre ciudades (horas):
Formulación
Variables Xij: Horas de
viaje desde la ciudad i hasta la ciudad j. Siendo i=A,B,C,D{1,2,3,4} y
j=A,B,C,D{1,2,3,4}
Solución
Para poder darle solución a
este problema se realizan cambios en el nombre de las variables se acomodan de
acuerdo a su posición del 1 al 12.
X1=X12
X6=X24
X7=X31
X12=X43
Por
lo tanto se dice que el recorrido será de siguiente manera:
Pasa
de la ciudad A a la B
Pasa
de la ciudad B a la D
Pasa
de la ciudad D a la 4
Pasa
de la ciudad C a la A terminando donde se inició el recorrido.
El tiempo mínimo usado
haciendo este recorrido será de 9 horas.
Elaborado por:
Fontiveros Alejandro
González Emeli
López Javier








No hay comentarios:
Publicar un comentario